Главная
Готовые работы
Теория вероятностей
Предмет: Теория вероятностей Дата публикации: 09.01.2015Размер файла: 751.5 Kb [zip]
2266
0

Постройте графики ряда распределения

Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн. руб.
№ предприятия Выпуск продукции Прибыль № предприятия Выпуск продукции Прибыль
1 61 15,7 16 52 14,6
2 78 18 17 62 14,8
3 41 12,1 18 69 16,1
4 54 13,8 19 85 16,7
5 61 15,5 20 71 15,8
6 26 17 21 71 16,4
7 45 12,8 22 36 27
8 57 14,2 23 72 16,5
9 67 15,9 24 88 18,5
10 81 17,6 25 71 16,4
11 92 18,2 26 74 16
12 48 12 27 96 19,1
13 59 16,5 28 75 16,3
14 68 16,2 29 101 19,6
15 81 16,7 30 71 17,2
 
По исходным данным:

1. Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте графики ряда распределения.

2. Рассчитайте числовые характеристики ряда распределения предприятий по сумме прибыли: среднюю арифметическую xb, среднее квадратическое отклонение, дисперсию, коэффициент вариации. Сделать выводы.

3. Определить границы, в которых с вероятностью 0,997 заключена сумма прибыли одного предприятия в генеральной совокупности.

4. Используя x2 - критерий Пирсона, при уровне значимости 0,05 проверить гипотезу о том, что случайная величина Х - сумма прибыли - распределена по нормальному закону.

5. Установите наличие и характер корреляционной связи между стоимостью произведенной продукции (Х) и суммой прибыли на одно предприятие (Y). Постройте диаграмму рассеяния и линию регрессии.

6. Определите коэффициенты выборочного уравнения регрессии 
 

 
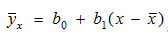
7. Рассчитайте линейный коэффициент корреляции. Используя t- критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами X и Y, используя шкалу Чеддока.
 


Стоимость: 250руб.

©Авторское исполнение от AllWorks.su

Яндекс.Деньги:
Банковская карта:
 

Поделиться в социальных сетях 
 



Войдите:
avatar