Бесконечно малые (б.м.) и бесконечно большие (б.б.) последовательности

Ключевые слова: пределы функций, лекции, свойство, математический анализ.

Определение. Последовательность (a_n) называется бесконечно малой, если

т.е. для любого ε>0 найдется номер N=N(ε) такой, что при всех n > N будет |a_n|<ε. Иначе, в любом интервале (-ε;ε) находится бесконечно много членов этой последовательности, а вне ее находится лишь конечное число членов.

Свойства б.м. последовательностей:

1) Сумма, разность и произведение двух б.м. последовательностей является б.м., т.е. если

, то

2) Произведение ограниченной последовательности на б.м. является б.м., т.е., если существует такое M>0 , что для всех номеров

, то

В частности, если c=const , то

Определение. Последовательность (a_n) называется расходящейся к плюс бесконечности (или положительной бесконечно большой), если для любого числа A>0 найдется номер N=N(A), такой что при всех n>N выполняется неравенство a_n>A. Иначе говоря, начиная с номера N+1 все члены последовательности, a_N+1, a_N+2, ..., лежат в интервале

а вне его может находиться лишь конечное число (не более N ) членов последовательности. Такая последовательность называется также стремящейся к

, что записывается так:

Аналогично, определяется

Определение. Последовательность (a_n) называется бесконечно большой (б.б.), если

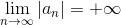Иначе говоря, для любого числа A>0 найдется номер N=N(A) такой, что все члены последовательности с номерами n>N находятся вне отрезка [-A; A], а внутри его лежит лишь конечное число членов последовательности. При этом пишут:

Связь между б.б. и б.м. последовательностями.

Пусть

– б.м., а

– б.б. последовательности, все члены которых отличны от нуля, тогда последовательность

будет б.б., а последовательность

– б.м.

Похожие материалы: