Исследовать на экстремум функцию

Ключевые слова: производные и дифференциалы, примеры решений задач.

Пример. Исследовать на экстремум функцию

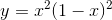
$y=x^2(1-x)^2$

Решение. Найдем точки, подозрительные на экстремум. Для этого возьмем производную y' и приравняем ее нулю.

На тех интервалах, где y' < 0, функция убывает; где y' > 0, функция возрастает. Поэтому интервалы возрастания функции

$\left ( 0, \frac{1}{2} \right )$ и $\left (1, \infty \right )$ ,

интервалы убывания функции

$\left ( -\infty , 0 \right )$ и $\left ( \frac{1}{2}, 1 \right )$

По рисунку видно, что в точках x=0 и x=1 функция принимает свои минимальные значения, а при x=1/2 - максимальное. Найдем эти значения:

Похожие материалы: