Основные комбинаторные формулы
Размещения. Размещениями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения. Число размещений из n элементов по m в каждом обозначается символом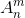 
и вычисляется по формуле
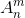и вычисляется по формуле
Смотреть пример...
Размещения с повторениями. Каждое размещение с повторениями из n элементов по m элементов может состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов, взятых из данных n элементов. Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями. Число размещений с повторениями из n элементов по m элементов обозначается символом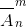
и вычисляется по формуле
Размещения с повторениями. Каждое размещение с повторениями из n элементов по m элементов может состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов, взятых из данных n элементов. Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями. Число размещений с повторениями из n элементов по m элементов обозначается символом
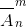и вычисляется по формуле
Смотреть пример...
Сочетания. Сочетаниями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним эле-ментом. Число сочетаний из n элементов по m в каждом обозначается символом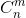
и вычисляется по формуле
Сочетания. Сочетаниями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним эле-ментом. Число сочетаний из n элементов по m в каждом обозначается символом
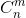и вычисляется по формуле
Смотреть пример...
Сочетания с повторениями. Сочетание с повторениями из n элементов по m элементов может содержать любой элемент сколько угодно раз от 1 до m включительно или не содержать его совсем, т.е. каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но из m каких угодно и как угодно повторяющихся элементов. Число сочетаний с повторениями из n элементов по m обозначают символом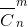
и вычисляют по формуле
Сочетания с повторениями. Сочетание с повторениями из n элементов по m элементов может содержать любой элемент сколько угодно раз от 1 до m включительно или не содержать его совсем, т.е. каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но из m каких угодно и как угодно повторяющихся элементов. Число сочетаний с повторениями из n элементов по m обозначают символом
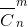и вычисляют по формуле
Смотреть пример...
Перестановки. Перестановками из n элементов называются такие соединения, из которых каждое содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов. Число перестановок из n элементов обозначается символом {Pn}, это то же самое, что число размещений из n элементов по n в каждом, поэтому
Перестановки. Перестановками из n элементов называются такие соединения, из которых каждое содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов. Число перестановок из n элементов обозначается символом {Pn}, это то же самое, что число размещений из n элементов по n в каждом, поэтому
Смотреть пример...
Перестановки с повторениями. Пусть имеются n элементов, среди которых k1 элементов одного типа, k2 элементов другого типа, kl элементов l-го типа k1+k2+...+kl=n. Число перестановок из этих n элементов равно числу перестановок с повторениями, обозначается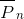
и вычисляется по формуле
Перестановки с повторениями. Пусть имеются n элементов, среди которых k1 элементов одного типа, k2 элементов другого типа, kl элементов l-го типа k1+k2+...+kl=n. Число перестановок из этих n элементов равно числу перестановок с повторениями, обозначается
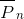и вычисляется по формуле
Похожие материалы:
Примеры решений задач
Готовые работы